Levy Distribution
Parameters
 - continuous scale parameter
(
- continuous scale parameter
(
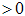 )
) - continuous location parameter
(
- continuous location parameter
( yields the one-parameter Levy distribution)
yields the one-parameter Levy distribution)
Domain

Two-Parameter Levy Distribution
Probability Density Function

Cumulative Distribution Function

One-Parameter Levy Distribution
Probability Density Function

Cumulative Distribution Function

where  is the
Laplace Integral.
is the
Laplace Integral.
Worksheet and VBA Functions
The following worksheet and VBA functions are available for this distribution:
| Distribution Fitting | - |
=DistFit("Levy";Data;[Options]1)
|
| Probability Density Function | LevyPdf(x,sigma,[gamma]) |
=LevyPdf(sigma;[gamma]) |
| Cumulative Distribution Function | LevyCdf(x,sigma,[gamma]) |
=LevyCdf(sigma;[gamma]) |
| Survival Function | LevySurv(x,sigma,[gamma]) |
=DistSurv("Levy(sigma;[gamma])";x)
|
| Hazard Function | LevyHaz(x,sigma,[gamma]) |
=LevyHaz(sigma;[gamma]) |
| Cumulative Hazard Function | LevyCumHaz(x,sigma,[gamma]) |
=DistCumHaz("Levy(sigma;[gamma])";x)
|
| Inverse CDF (Quantile Function) | LevyInv(P,sigma,[gamma]) |
=LevyInv(sigma;[gamma]) |
| Random Numbers | LevyRand(sigma,[gamma]) |
=LevyRand(sigma;[gamma]) |
| Mode | LevyMode(sigma,[gamma]) |
=DistMode("Levy(sigma;[gamma])")
|
-
The
Optionsparameter is optional. Possible options: "gamma=value" (example: "gamma=0") -
The
gammaparameter is optional (the default value is 0).
www.mathwave.com

