Continuous Distributions

Distribution Types

EasyFit supports a number of continuous distributions divided into four categories (distribution types):

• bounded;
• unbounded;
• non-negative;
• advanced.

Bounded Distributions

The bounded distributions have a range of [a, b]:

• Beta
• Johnson SB
• Kumaraswamy
• Pert
• Power Function
• Reciprocal
• Triangular
• Uniform

Unbounded Distributions

The unbounded distributions have a range of (-Infinity, +Infinity):

• Cauchy
• Error
• Error Function
• Gumbel Max
• Gumbel Min
• Hyperbolic Secant
• Johnson SU
• Laplace (Double Exponential)
• Logistic
• Normal
• Student's t

Non-Negative Distributions

Most of the non-negative distributions are defined for, so , where (gamma) is a continuous location parameter.

The non-negative distributions can be simplified if we set the location parameter to a fixed value of 0. This simplified form is quite frequently used in many applications. However, in certain cases the inclusion of the location parameter allows to develop more valid models. For example, both two-parameter and three-parameter Weibull distributions are widely used in practice.

Thus, most supported non-negative distribution are available in two different forms, or versions: full and simplified (see Fitting Non-Negative Distributions).

EasyFit supports the following non-negative distributions:

Distribution	Parameters
	Simplified Form	Full Form
Burr	, ,	, , ,
Chi-Squared		,
Dagum	, ,	, , ,
Erlang	,	, ,
Exponential		,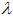
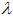F Distribution	,
Fatigue Life (Birnbaum-Saunders)	,	, ,
Frechet	,	, ,
Gamma	,	, ,
Generalized Gamma	, ,	, , ,
Inverse Gaussian	,	, ,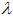
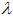Levy		,
Log-Gamma	,
Log-Logistic	,	, ,
Lognormal	,	, ,
Nakagami	,
Pareto (First Kind)	,
Pareto (Second Kind)	,
Pearson Type 5	,	, ,
Pearson Type 6	, ,	, , ,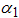
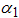Rayleigh		,
Rice	,
Weibull	,	, ,

Advanced Distributions

Since the classification of continuous distributions used in EasyFit is based on the range of definition, some of them do not fall into any of the above mentioned categories. At the same time, they often represent much more valid models than many other distributions. The following advanced distributions are supported:

• Generalized Extreme Value
• Generalized Logistic
• Generalized Pareto
• Log-Pearson 3
• Phased Bi-Exponential
• Phased Bi-Weibull
• Wakeby

The phased distributions are mainly utilized in reliability analysis, while the Wakeby distribution is widely used for the modelling of extreme events. Each of the supported generalized distributions combines two or more simpler distributions. For example, the generalized extreme value (GEV) distribution combines the Gumbel, Frechet, and Weibull families.